In this article, we will solve Leetcode problem number: 509. Fibonacci Number
Problem statement:
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1. Given n, calculate F(n).
What is Fibonacci Number?
The Fibonacci numbers are a sequence of numbers in mathematics named after Leonardo of Pisa, known as Fibonacci. The first number of the pattern is 0, the second number is 1, and each number after that is equal to adding the two numbers right before it together. (Source: Wikipedia)
F(0) = 0, F(1) = 1
F(2) = F(0) + F(1) = 0 + 1 = 1
F(3) = F(2) + F(1) = 1 + 1 = 2
F(n) = F(n-1) + F(n-2) ---> equation no. 1
Thought Process:
In order to solve this problem recursively, we need to write:
- Base case
- Recurrence relation (an equation that recursively defines a sequence where the next term is a function of the previous terms)
Since we already know the value of F(0) and F(1), we will use them as our base cases:
def fib(self, n: int) -> int:
#base case
if n == 0:
return 0
if n == 1:
return 1
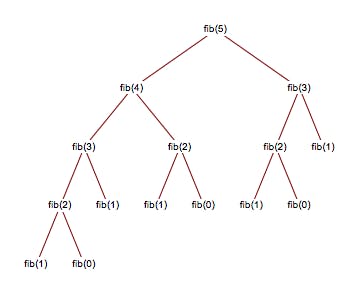
Equation number 1 above can act as recurrence relation for this problem. Because it will break all cases into small chunks and make use of our base cases. Take for instance F(4): Our recurrence relation = F(n) = F(n-1) + F(n-2)
F(4) = F(3) + F(2)
Using recurrence relation to calculate F(3) and F(2). It can further be written as:
F(4) = [ F(2) + F(1) ] + F(2) ---> equation no.2
F(4) = [ F(2) + F(1) ] + [ F(1) + F(0) ]
Again using recurrence relation to calculate F(2)
F(4) = [ F(0) + F(1) + F(1) ] + [ F(1) + F(0) ]
It is clear that our recurrence relation is breaking the problem till it reaches the bases cases. To write a recursive function we will simply call our function in accordance with our recurrence relation till we reach the base case. After combining our base case and recurrence relation, it will be very easy for us to write our final piece of code! 😎
def fib(self, n: int) -> int:
#base case
if n == 0:
return 0
if n == 1:
return 1
# use recurrence relation and call
# our function recursively, for all other cases
else:
return self.fib(n-2) + self.fib(n-1)
Note: This is not the optimized way to solve the problem on Fibonacci number. It is because, if you observe 'equation number 2' above, you will see we are calculating value of F(2) twice. One way to handle this problem is to store the values beforehand and then use them, thereby eliminating the need of recalculation.
But anyways, this problem helps us understand the concept of recursion very well.
If you follow along the series, congratulations! you solved 3 easy level problems of leetcode on recursion!! 🥳💃💃
